Recently on Ernst Baart’s Hockey Site, Fede Tanuscio gave another interesting Masterclass, this time on what he called ‘Circle Priorities’.
Fede’s focus was on how to prioritise playing actions depending on the area of the circle the player happens to be in. Here, for example, are his circle divisions along with the sort of actions one might expect to be chosen in each area.
There are many more good things in Fede’s talk and I would urge you to go and watch it, but during the Masterclass I began to think about the choices faced by the attackers. Much emphasis is placed on shooting. The top left and right sections of Fede’s circle not only prescribes this in-circle action but also suggests what kind of technique to use for the shot. This is all good, it is the pumping heart of hockey, get into the circle and shoot.
But, to state the ‘bleedin’ obvious’, not all circle entries lend themselves to getting a shot away. Alyson Annan in a previous Masterclass, specifically talked about shooting and actions that created shooting opportunities, passing to shoot being a notable phrase. So there are decisions to be made, even in areas that are regarded as prime shooting real estate, about how much a player should persist in trying to manufacture a shot rather than seeking some alternative action (a pass to shoot, a penalty corner etc).
The question then is, do players make good decisions in the circle when it comes to shooting or does the desire to shoot sometimes get in the way of a more pragmatic approach?
How to look at this? To start, and rather than treating each shot as a fait accompli, it would be good to know not only know where shots were taken from, but also the circumstances surrounding each of those shots. For this we can use the data from the last Olympics (the women’s game) and to make life easier pick just one of Fede’s pitch sections.
These are all the shots taken during the women’s 2024 Olympics in the top right hand corner of the circle. I’m guessing a bit at the exact dimensions Fede used for his sections in Figure 2 but it looks close enough for this discussion. There were, as you can see, 131 shots. Are all those shots equal? Do they all contribute the same to their teams attacking potency? No, of course they aren’t and any of you who have read previous articles here will know what is coming next.
Using an ‘expected Goals’ (xG) model (see here and watch this talk) we can assign a value to each of these shots - the probability that the shot will become a goal.
And obviously the model indicates that, no, not all shots1 are equal. The size of the circle representing each shot is related to the value of the shot, the larger the circle the higher the probability of scoring. The frequency distribution of these values looks like this.
The median probability2 of any of these shots becoming a goal from this top right hand section of the circle is just 7.5% - the dashed red line. Really not very high at all and the peak of the distribution is lower at 5%.
Goals were scored in this area during the Olympics, it is not some peculiar goal scoring desert, and we can show where these occurred.
The white circles are now the goal scoring shots. Overall the highest probability value for a shot in this section is 68% (Rocio Sanchez Moria for Argentina against the United States) and the lowest 1.7% (an attempt by Charlotte Englebert for Belgium against Germany), but note that though the median value of goal scoring shots is more than twice as high as shots that didn’t score this is still quite a low xG value. The equivalent metrics for Fede’s central square in front of goal (see Figure 2 - Push/Deflection section) is 21% and 55% for non-scoring and scoring shots respectively.
There are reasons why shot values are generally low in this top right section. For one, they are taken from further away and at a worse angle than in front of goal. In addition, there is variation in xG value (circle size) that comes from factors like the amount of pressure the attacker is under, the type of shot used etc.
Decision making based on knowledge of the value of the shot a player is about to take - even as a rough, experience informed estimate, would seem to be important. To emphasise this here’s something I heard during a game in the football European Cup over the summer. The game was Denmark against England and in the first half the Danish player, Morten Hjulmand, scored a screamer, a strike from about 30 metres, that put the Danes a goal up. It just so happened that in the Match of the Day studio sitting alongside Gary Lineker was Thomas Frank, the Danish head coach of the English Premiership club, Brentford. Naturally his opinion was sought at half time on his compatriot’s wonder goal. His first remark was enlightening, “Well,” he said, “I wouldn’t have told him to take that shot,… but still, it was a lovely goal”. Here is the realpolitik of football coming up against the emotional catharsis of such a goal.
Thomas Frank’s point was that the probability of Hjulmand scoring was low and generally he would have done better to look for an alternative action. In light of this, and knowing the xG values of shots from the top right of the circle during the Olympics, the question might well be posed - why on earth are we shooting from here at all? After all, scoring a goal is rare despite this apparently being a shot making area of the circle, and the probability of scoring is remote.
Perhaps we should ignore shooting. Instead we could ask our players to deliberately not shot when they get into this part of the circle. Not shoot, but execute an alternative action that increases the probability of scoring. One way to do that is to win corners. If players did this, if the shots taken were changed to corners won, the outcome looks quite different.
In principle, Figure 7 is similar to Figure 4. Each circle is now a penalty corner instead of the original shot and the size of the circle represents the expected Penalty Corner Goal (xPCG) value. This value is simply derived from each team’s penalty corner conversion rate across the whole tournament. Hence, if the Netherlands get into this area of the circle and win a corner instead of one of the shots they did actually take, they would be rewarded with an xPCG of 0.28. And the same for each and every time they would have taken a shot but won a corner instead. The range of conversion rates (and so circle size) goes from those super efficient Dutch, through Great Britain with a much more mundane rate (0.11 - ho hum) and down to Spain who only managed to score 5% of their corners3.
Is this better than taking shots? For the Olympics the cumulative xG estimate is 14 goals scored for all those shots taken in the top right hand corner (Figure 4). The number of goals actually scored from this area was 154. Now, if we add up the xPCG values that have been substituted for the shots we get 23 goals, a much better return for in-circle actions than shooting.
Is this realistic? Can we change the philosophy of hockey and make a priority of the winning and subsequent execution of the sports unique set-piece rather than what it is now, a game about the visceral excitement of shooting with other circle actions an accidental or, at the most, secondary consideration?
And it does raise some questions not least being whether corners are really ‘won’ or are actually ‘awarded’. This is a slight sideline for another article but a brief look suggests that corners are not often deliberately ‘won’ by the attackers. It is not a priority for them (as finding space for a shot is) and the majority of the corners occur as the outcome of other actions (passes in or into the circle, defensive errors, rebounds, accidents). So there is a question about whether corners can be won at a similar rate to shots taken.
But, let’s leave that aside for another post and ask whether there is a slightly more nuanced approach we can follow. Perhaps converting all the shots taken into corners is unrealistic. What we should be asking is what the outcome would be if players made better decisions about shooting. To do this we need to know more detail about what happens to all these shots.
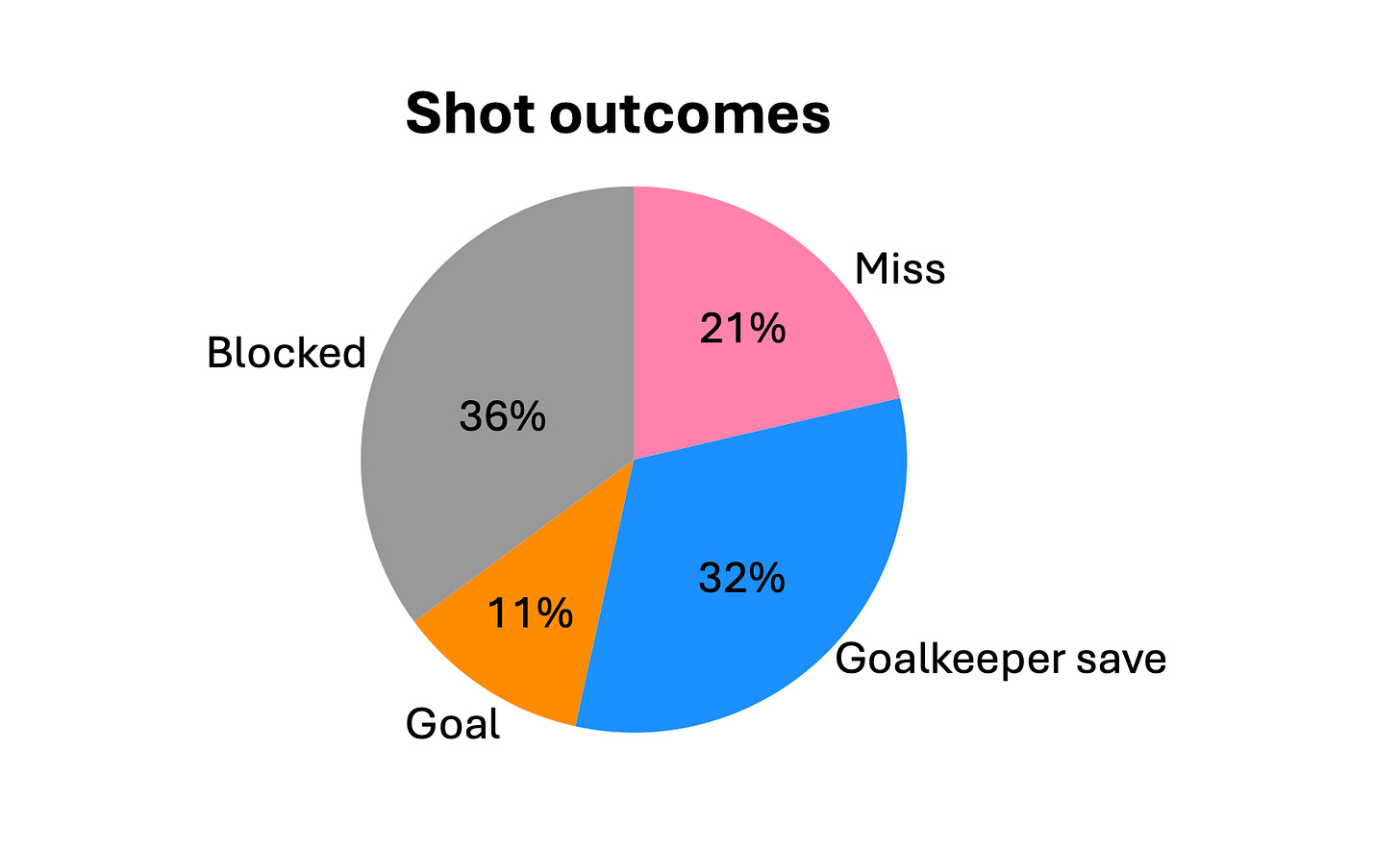
And here it is, again just for Fede’s top right corner. The categories are obvious except perhaps for “Blocked” which here indicates shots that were blocked or smothered by a defender before it reached the goal. In the majority of cases these blocks are made close to the attacker by the defender(s) pressure. Median shot values for these categories are 0.052, 0.08, 0.16, 0.086 for ‘Blocked’, ‘Goalkeeper save’, ‘Goal’ (as we’ve seen on Figure 6) and ‘Miss’ respectively.
If we are generous we might allow that any shot which reaches the goal is the result of both a good decision by the attacker as well as competent execution. So we keep those and encourage players in similar situations to take a shot. What we change is those shots that were blocked. It’s clear that these shots have a lower xG value (just 5.2%) than the other categories and the attacker likely could tell their shot would be under pressure from close defenders. The decision to change the action from a shot to a more productive outcome should be relatively easy. What happens then if we just change those blocked shots for corners and keep all the shots that turned into goals and goalkeeper saves?
There is still some room for improvement (isn’t there always) and some of the shot values are still low and the overall value is not as good as turning all shots into corners. But, it is still better than the actual outcome of the 131 shots taken from this area during the Olympics by four goals.
So should we be thinking more probabilistically? Should we be looking at chance creation in terms of their value and asking players to make better decisions in the circle (this area of the circle at least5) and providing them with the techniques to maximise their circle entry outcomes. To do so runs the risk of being labelled a bean counter, of taking the joy in uncertainty from the game. Worse, one might end up being described as a “laptop coach” - a pejorative phrase ascribed to the young cohort of German football coaches (Nagelsmann, Tedesco et al.) who, so some complain, never get their heads out of their computers long enough to sniff the traditional sweat, simulation and swearing of football. And many coaches will say that they do ask players to make good decisions in the circle. The evidence from the Olympics though, is that there are still better decisions to be made.
And above all this, I may be wrong. I might have misrepresented shooting. That despite everything a shot implies, it is not a one and done endeavour. The shot is actually the starting point of a sequence of attacking possibilities because though a shot only occasionally scores a goal from this area of the circle, it may work as the catalyst for subsequent goalscoring actions. All those shots that are scuffed, topped, botched in some way; all those shots that are blocked by a defender, blocked by an attacker, come back off the post or crossbar and those ultimately saved by the goalkeeper, are all a product of that first attempt to get the ball going towards goal and the aftermath, the spillage from that attempt, could result in subsequent positive actions. Looked at this way, a shot is the start of an accumulation of goal scoring values and not an end in and of itself as it is often treated.
To see if that is true requires tracking not only the shot itself but what happens next. That requires another analysis and I’ll talk about those results in another article.
And I should be very clear here that the interest is really in decision making so ‘shot’ really is shot attempt. The shot attempt may score a goal but equally it may be blocked by a defender or even fluffed and miss by metres. The point is that the attacker has made the decision to shoot over and above any other actions they might also have made.
Median because this is highly skewed data (see Figure 5) with the values bunched up on the left of the graph (it is right skewed in the rather counter intuitive statistical terminology). With this data the average value (as I have erroneously reported before) can be heavily influenced by a few high values giving an unrealistic measure of the central tendency. The median is more informative in these cases.
In general xPCG values are higher than xG values. But there can be a crossover when a teams xPCG is lower than their xG - particularly in tournament play. But bear with me, for the purpose of this article I’m going to ignore that little point. And actually for Spain the difference isn’t that great (0.07 for xG, 0.05 for xPCG).
Yay for the xG model!
The other areas Fede divided the circle into will differ. As noted in the main text shooting from the central area close to goal has higher xG values. Shooting from one of the lower areas likely worse values. What might be interesting is to see whether goal scoring and xG values differ depending on which side of the circle the action is taken from. Is there any left-right bias?